자기 모멘트

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
- 2.1. 자기 쌍극자 모멘트
- 2.2. 에너지 관점에서의 정의
3. 단위
4. 자기장과의 상호작용
- 4.1. 돌림힘
- 4.2. 위치 에너지
5. 자기 쌍극자의 자기장
6. 자기화와의 관계
7. 자기 모멘트의 모델
8. 원자, 분자, 소립자의 자기 모멘트
9. 외부 자기장 효과
10. 자기 쌍극자 간의 상호작용
- 10.1. 두 자기 쌍극자 사이의 힘
- 10.2. 토크
11. 자기 쌍극자의 이론적 배경
12. 각운동량과의 관계
13. 같이 보기
14. 외부 링크
15. 참고 문헌
16. 각주
참조

1. 개요

자기 모멘트는 전류 흐름이나 소립자의 스핀으로 인해 발생하는 자기 쌍극자의 자기적 특성을 나타내는 벡터량이다. 자기 모멘트는 물체에 작용하는 정렬 토크를 자기장과 관련시키는 데 사용되며, 국제단위계(SI)에서는 암페어 제곱미터(A·m²) 또는 줄 매 테슬라(J/T)로, CGS 단위계에서는 에르그 매 가우스(erg/G)로 측정된다. 자기 모멘트는 원자, 분자, 소립자의 자기적 성질을 이해하는 데 중요한 역할을 하며, 외부 자기장과의 상호 작용, 자기 쌍극자 간의 상호 작용, 각운동량과의 관계 등 다양한 물리적 현상을 설명하는 데 활용된다.

더 읽어볼만한 페이지

모멘트 (물리학) - 각운동량
각운동량은 회전 운동량을 나타내는 물리량으로, 질점의 경우 위치 벡터와 선운동량의 벡터곱으로 정의되며, 외부 토크가 없을 때 보존되고, 양자역학에서는 양자화되는 특성을 지닌다.
모멘트 (물리학) - 운동량
운동량은 물체의 질량과 속도의 곱으로 정의되는 벡터량으로, 외부 힘이 작용하지 않는 계에서는 보존되며, 충돌, 충격량, 질량 변화, 상대론, 해석역학, 전자기학, 양자역학 등 다양한 역학 분야에서 중요한 물리량으로 다뤄진다.
자기 - 상자성
상자성은 외부 자기장이 없을 때는 자성을 띠지 않지만, 외부 자기장이 가해지면 자기장 방향으로 약하게 자화되는 성질을 말하며, 짝을 짓지 않은 전자의 스핀으로 인해 영구 자기 모멘트를 가지는 상자성체가 이러한 특징을 보인다.
자기 - 자석
자석은 내부 자구들의 정렬로 자기장을 생성하는 물체로, N극과 S극을 가지며 영구자석과 전자석으로 나뉘어 나침반, 스피커 등 다양한 분야에 활용된다.
전기 - 전기장
전기장은 공간의 각 지점에서 단위 전하가 받는 힘으로 정의되는 벡터장으로, 전하 또는 시간에 따라 변하는 자기장에 의해 발생하며, 전기력선으로 표현되고 맥스웰 방정식으로 기술되는 전자기장의 한 요소이다.
전기 - 전압
전압은 두 지점 사이의 전위차로서 단위 전하당 에너지 차이를 나타내며, 정전기학에서는 단위 전하를 이동시키는 데 필요한 일, 회로 이론에서는 노드 간 전위차로 정의되고, 직류 및 교류 전압으로 구분되며, 다양한 방식으로 발생하여 여러 분야에 응용된다.

자기 모멘트
일반 정보
명칭	자기 모멘트
영어 명칭	magnetic moment
정의	자기장을 생성하는 물체의 자기 강도 및 방향
종류	자기 쌍극자 모멘트
관련 분야	전자기학, 정자기학
기호 및 단위
기호	m
SI 단위	암페어-미터² (A⋅m²) = 줄/테슬라 (J/T)
유도 단위	미터²⋅암페어 (m²⋅A)
차원	L²I
추가 정보
관련 항목	다중극 전개
자기 퍼텐셜 에너지	U = -m ⋅ B

2. 정의

면적 $S$ 와 전류 $I$ 를 지닌 평면 전류고리의 자기 모멘트 $\mathbf m$ .

전류 밀도

\mathbf J

가 흐르는 물체가 있다고 하자. 그렇다면 이 물체의 '''자기 모멘트'''

\mathbf m

는 다음과 같다.

:

\mathbf m=\frac12\int\mathbf r\times\mathbf J\,dV

.

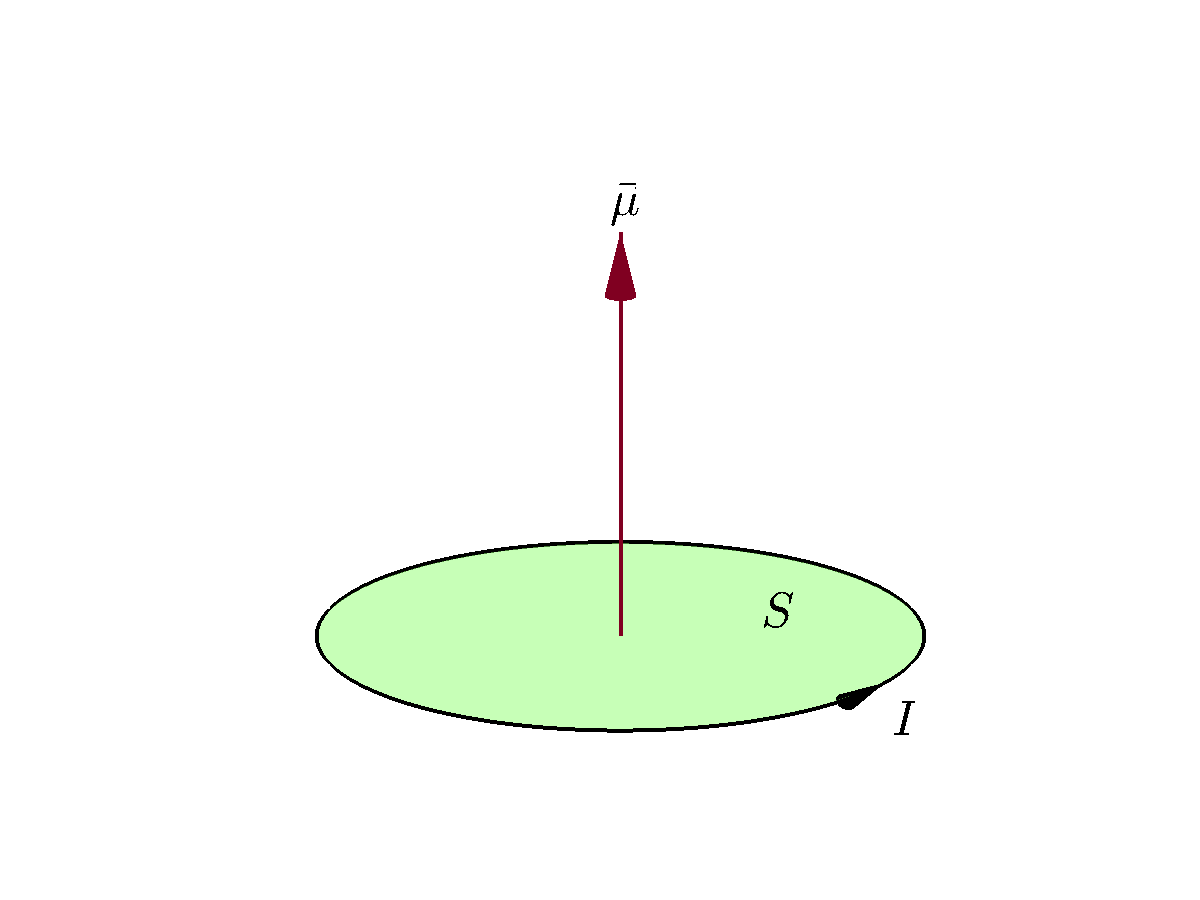
이 공식의 특수한 경우로, 평면 상에 면적

S

인 폐곡선을 따라 흐르는 전류

I

를 생각해 보자. 그렇다면 전류 고리의 자기 모멘트는 다음과 같다.

:

\mathbf m=IS\hat{\mathbf n}

.

여기서

\hat{\mathbf n}

는 평면에 수직인 단위벡터이며, 전류에 대해 오른손 규칙을 따른다. 즉, 엄지를 곧게 세우고 전류의 방향으로 오른손 네 손가락을 감아 쥐었을 때 엄지손가락이 가리키는 방향이 곧 자기 모멘트의 방향이다.

만약 폐곡선을 평면 위에 놓을 수 없다면, 일반적인 공식

:

\mathbf m=\frac12I\oint\mathbf r\times d\mathbf r

을 써야만 한다.

자기 모멘트는 외부에서 가해진 자기장으로부터 물체에 작용하는 정렬 토크를 자기장 벡터 자체와 관련짓는 벡터(사실은 유사 벡터)로 정의할 수 있다.^[1]

:

\boldsymbol{\tau} = \mathbf{m} \times\mathbf{B}

여기서 는 쌍극자에 작용하는 토크이고, 는 외부 자기장이며, 은 자기 모멘트이다.

열역학 계산에서 자기 모멘트에 유용한 대안적인 정의가 있다. 이 정의에서 계의 자기 쌍극자 모멘트는 고유 에너지 의 외부 자기장에 대한 음의 기울기이다.

:

\mathbf{m} = -\hat\mathbf x \frac{\partial U_\text{int}}{\partial B_x} - \hat\mathbf y \frac{\partial U_\text{int}}{\partial B_y} - \hat\mathbf z \frac{\partial U_\text{int}}{\partial B_z}.

일반적으로 고유 에너지는 계의 자체장 에너지와 계의 내부 작용 에너지를 포함한다. 예를 들어, 외부장에 있는 2p 상태의 수소 원자의 경우 자체장 에너지는 무시할 수 있으므로 내부 에너지는 본질적으로 쿨롱 전위 에너지와 전자의 운동 에너지를 포함하는 2p 상태의 고유 에너지이다. 내부 쌍극자와 외부장 사이의 상호 작용장 에너지는 이 내부 에너지에 포함되지 않는다.^[2]

국제단위계에서 자기 모멘트의 단위는 암페어 제곱 미터 (A·m²) 또는 줄 매 테슬라(J/T)이다. 이 둘은 같은 단위의 서로 다른 이름이다. 첫 번째 이름은 자기 모멘트가 전류와 면적의 곱이라는 공식을 나타내고, 두 번째 이름은 자기 모멘트가 자기적 위치 에너지와 외부 자기장의 비라는 공식을 나타낸다.

CGS 단위계에서는 보통 에르그 매 가우스(erg/G)를 쓰고, 이는 줄 매 테슬라의 1000분의 1이다. 즉, 국제단위계로 환산하면 다음과 같다.

:1 erg/G = 1 mJ/T = 1 mA·m².

2. 1. 자기 쌍극자 모멘트

전류 밀도 J가 흐르는 물체의 '''자기 모멘트''' m은 다음과 같이 정의된다.^[9]

:

\mathbf m=\frac12\int\mathbf r\times\mathbf J\,dV

.

여기서 ×는 벡터 외적, r은 위치 벡터이고, j는 전류 밀도이며, 적분은 체적분이다.^[9]

평면 상에 면적 ''S''인 폐곡선을 따라 흐르는 전류 ''I''를 생각해 보자. 그렇다면 전류 고리의 자기 모멘트는 다음과 같다.

:

\mathbf m=IS\hat{\mathbf n}

.

여기서

\hat{\mathbf n}

는 평면에 수직인 단위벡터이며, 전류에 대해 오른손 규칙을 따른다. 즉, 엄지를 곧게 세우고 전류의 방향으로 오른손 네 손가락을 감아 쥐었을 때 엄지손가락이 가리키는 방향이 곧 자기 모멘트의 방향이다.

만약 폐곡선을 평면 위에 놓을 수 없다면, 일반적인 공식

:

\mathbf m=\frac12I\oint\mathbf r\times d\mathbf r

을 써야만 한다.

자기 모멘트는 외부에서 가해진 자기장으로부터 물체에 작용하는 정렬 토크를 자기장 벡터 자체와 관련짓는 벡터(사실은 유사 벡터)로 정의할 수 있다.^[1]

\boldsymbol{\tau} = \mathbf{m} \times\mathbf{B}

여기서 는 쌍극자에 작용하는 토크이고, 는 외부 자기장이며, 은 자기 모멘트이다.

열역학 계산에서 자기 모멘트에 유용한 대안적인 정의가 있다. 이 정의에서 계의 자기 쌍극자 모멘트는 고유 에너지 의 외부 자기장에 대한 음의 기울기이다.

\mathbf{m} = -\hat\mathbf x \frac{\partial U_\text{int}}{\partial B_x} - \hat\mathbf y \frac{\partial U_\text{int}}{\partial B_y} - \hat\mathbf z \frac{\partial U_\text{int}}{\partial B_z}.

2. 2. 에너지 관점에서의 정의

자기 모멘트는 계의 고유 에너지 의 외부 자기장에 대한 음의 기울기로 정의할 수 있다.^[2]

:

\mathbf{m} = -\hat\mathbf x \frac{\partial U_\text{int}}{\partial B_x} - \hat\mathbf y \frac{\partial U_\text{int}}{\partial B_y} - \hat\mathbf z \frac{\partial U_\text{int}}{\partial B_z}.

일반적으로 고유 에너지는 계의 자체장 에너지와 계의 내부 작용 에너지를 포함한다. 예를 들어, 외부장에 있는 2p 상태의 수소 원자의 경우 자체장 에너지는 무시할 수 있으므로 내부 에너지는 본질적으로 쿨롱 전위 에너지와 전자의 운동 에너지를 포함하는 2p 상태의 고유 에너지이다. 내부 쌍극자와 외부장 사이의 상호 작용장 에너지는 이 내부 에너지에 포함되지 않는다.^[2]

자기장

\mathbf{B}

하에서 길이

\mathbf{L}

의 직선 전류

\mathbf{i}

가 받는 힘은

:

\mathbf{F} = \mathbf{iL}\times\mathbf{B}

임을 이용하면, 임의의 모양을 지닌 전류 고리에 대해서도 자기 모멘트를 정의 할 수 있다. 이때, 자기 모멘트는 외부에서 가해진 자기장으로부터 물체에 작용하는 정렬 토크를 자기장 벡터 자체와 관련짓는 벡터(사실은 유사 벡터)로 정의된다.^[1]

:

\boldsymbol{\tau} = \mathbf{m} \times\mathbf{B}

여기서 는 쌍극자에 작용하는 토크이고, 는 외부 자기장이며, 은 자기 모멘트이다.

3. 단위

국제단위계(SI)에서 자기 모멘트의 단위는 암페어 제곱미터(A·m²) 또는 줄 매 테슬라(J/T)이다.^[3]^[4] 이 둘은 같은 단위의 서로 다른 이름이다. A⋅m²는 자기 모멘트가 전류와 면적의 곱이라는 공식을 나타내고, J/T는 자기 모멘트가 자기적 위치 에너지와 외부 자기장의 비라는 공식을 나타낸다. 자기 모멘트의 국제단위계 기본 단위는 A⋅m²이다. 여기서 A는 암페어(전류의 SI 기본 단위)이고 m은 미터(거리의 SI 기본 단위)이다. 이 단위는 N⋅m/T = J/T 와 같은 관계를 갖는다.^[5]

CGS 단위계에서는 에르그 매 가우스(erg/G)를 쓰며, 1 erg/G = 1 mJ/T = 1 mA·m²이다. 센티미터 그램 초 단위계에는 ESU, 가우스 단위계, 그리고 EMU가 있고, 이들 중 자기 쌍극자 모멘트의 두 가지 단위는 다음과 같다.

:1 statA⋅cm² = 3.33564095 × 10⁻¹⁴ A⋅m² (ESU)

:1 erg/G = 10⁻³ A⋅m² (가우스 단위계 및 EMU)

여기서 statA는 스탯암페어, cm은 센티미터, erg는 에르그, G는 가우스이다.

자기 쌍극자 모멘트를 측정하는 다른 단위로는 보어 마그네톤과 핵 마그네톤이 있다.

4. 자기장과의 상호작용

외부 자기장이 존재할 때, 자기 모멘트는 자기장으로부터 토크를 받는다. 이 토크에 의해 발생하는 세차운동은 라모어 세차라 불리며, 그 운동 방정식은

: $\frac{1}{\gamma} \frac{\mathrm{d}\boldsymbol{m}}{\mathrm{d}t} = \boldsymbol{m} \times \boldsymbol{H}$

로 나타낼 수 있다. 여기서, '''m'''은 자기 모멘트, '''H'''는 자기장, γ는 자기 회전 비율이다.

이에 더하여, 실제 물질 내의 세차운동은 시간이 지남에 따라 감쇠한다. 이러한 거동은 란다우-리프시츠-길버트 방정식에 의해 기술된다.^[30]^[31]

: $\frac{1}{\gamma} \frac{\mathrm{d}\boldsymbol{m}}{\mathrm{d}t} = \boldsymbol{m} \times \boldsymbol{H}_{\text{eff}} - \frac{\lambda}{\gamma m}\boldsymbol{m} \times \frac{\mathrm{d}\boldsymbol{m}}{\mathrm{d}t}.$

여기서, '''H'''_eff는 유효 자기장(외부 자기장 + 자체 자기장 + 양자역학적 보정), λ는 감쇠 운동의 크기를 결정하는 계수이다. 우변 제1항은 유효 자기장에 의한 자기 모멘트의 세차 운동을 나타내고, 제2항은 주위와의 상호작용에 의한 에너지 손실을 나타내는 감쇠항이다.

4. 1. 돌림힘

자기 모멘트 m를 지닌 전류 고리가 자기장 B 하에 놓이면 그 기하학적 중심에 대하여 알짜 돌림힘 τ가 작용한다.^[8] 이들 사이의 관계는 벡터의 벡터곱을 사용하여 다음과 같이 표현된다.

'''τ''' = '''m'''×'''B'''

이 식은 자기장이 균일하다면 국소적인 전류 분포에 의한 모멘트에 대해 유효하다. 균일하지 않은 B에 대해서는 자기 쌍극자가 충분히 작다면 자기 쌍극자의 중심에 대한 토크에 대해서도 유효하다.^[8]

균일한 자기장에 놓인 전자, 원자핵 또는 원자는 라모어 주파수로 알려진 주파수로 세차 운동을 한다. 핵자기 공명 참조.

외부 자기장이 존재할 때, 자기 모멘트는 자기장으로부터 토크를 받는다. 이 토크에 의해 발생하는 세차운동은 라모어 세차라 불린다.

이에 더하여, 실제 물질 내의 세차운동은 시간이 지남에 따라 감쇠한다. 이러한 거동은 란다우-리프시츠-길버트 방정식에 의해 기술된다.^[30]^[31]

4. 2. 위치 에너지

자기 모멘트 m을 지닌 전류 고리가 자기장 B 하에 놓이면, 자기 모멘트의 회전에 대하여 돌림힘에 의한 위치 에너지 U를 가진다. 이 에너지는 자기 모멘트와 자기장이 이루는 각 θ에 의존하며, 돌림힘과 자기장이 수직일 때 U = 0 이다. 이 관계는 벡터의 내적을 사용하여 다음과 같이 표현된다.

:U(θ) = -m ⋅ B외부 자기장이 존재할 때, 자기 모멘트는 자기장으로부터 토크를 받아 세차운동을 한다. 이 운동은 라모어 세차라 불린다.

실제 물질 내의 세차운동은 시간이 지남에 따라 감쇠하며, 이는 란다우-리프시츠-길버트 방정식으로 기술된다.^[30]^[31]

5. 자기 쌍극자의 자기장

시간에 따라 변하지 않는 자기 모멘트 m을 가진 자기 쌍극자의 벡터 퍼텐셜 A는 다음과 같다.

: $\mathbf A(\mathbf r)=\frac{\mu_0\mathbf m\times\hat{\mathbf r}}{4\mathrm\pi r^2}$ .

여기서 r은 쌍극자의 위치에서부터 퍼텐셜을 측정하려는 위치를 가리키는 변위 벡터이고, $\hat{\mathbf r}$ 은 r 방향의 단위벡터다. $\mu_0$ 은 진공의 투자율이다.

자기 쌍극자의 자기장 B(r)은 다음과 같다.

: $\mathbf{B}({\mathbf r}) = \nabla\times\mathbf{A} = \frac{\mu_0}{4\pi}\left(\frac{3\mathbf{r}(\mathbf{m} \cdot\mathbf{r})}{r^5} - \frac{\mathbf{m}}{r^3}\right)$ .

이는 자기 쌍극자 모멘트 m을 갖는 모든 계가 계를 둘러싼 공간에 생성하는 쌍극자 자기장에 대한 설명과 동일하며, 거리에 따라 자기장의 세기가 감소하는 정도 또한 동일하다. 앙페르 루프 모델에서 자기 선속 밀도는 다음과 같이 나타낼 수 있다.^[7]

: $\mathbf{B}(\mathbf{r}) = \nabla\times{\mathbf{A}} = \frac{\mu_{0}}{4\pi}\left(\frac{3\mathbf{r}(\mathbf{m}\cdot\mathbf{r})}{|\mathbf r|^5}-\frac}{|\mathbf r|^3}\right).$

자기 쌍극자에 대한 모델은 자기 극 또는 전류 고리가 있으며, 자기장의 근원으로부터 멀리 떨어진 곳에서는 두 모델이 동일한 예측을 제공한다. 그러나 근원 내부에서는 서로 다른 예측을 제공하는데, 극 사이의 자기장은 자기 모멘트와 반대 방향이고, 전류 고리 내부에서는 같은 방향이다.^[7] 만약 전류 고리를 점점 작게 만들면서 전류와 면적의 곱을 일정하게 유지하여 자기 쌍극자를 형성한다면, 한계 자기장은 다음과 같다.^[7]^[9]

: $\mathbf{B}(\mathbf{r})=\frac{\mu_0}{4\pi}\left[\frac{3\mathbf\hat{r}(\mathbf\hat{r}\cdot \mathbf{m})-\mathbf{m}}$

6. 자기화와의 관계

자기화 '''M'''은 단위 부피당 자기 모멘트로 정의된다.^[6] 균일한 자기화의 경우, 자기 모멘트 '''m'''은 다음과 같이 표현된다.:

\mathbf{m} = \mathbf{M} V,

여기서 ''V''는 자석의 부피이다.

일반적으로 자기화는 강자성체 재료의 매개변수로 사용되지 않고, 잔류 자속 밀도 (혹은 잔류 자기) '''B'''_r로 표시되는 경우가 많다. 이때 자기 모멘트 '''m''' (A⋅m² 단위)는 다음과 같이 계산한다.^[6]

:

\mathbf{m} = \frac{1}{\mu_0}\mathbf{B}_\text{r} V,

여기서:

'''B'''_r은 테슬라로 표현된 잔류 자속 밀도이다.
''V''는 자석의 부피(m³)이다.
''μ''₀는 진공의 투자율()이다.^[6]

7. 자기 모멘트의 모델

자기 모멘트에 대한 고전적인 설명은 시간이 지남에 따라 변해왔다. 1930년대 이전에는 교과서에서 가상의 자기 점전하를 사용하여 자기 모멘트를 설명했다.^[7] 그 이후로는 대부분 앙페르 전류를 이용하여 정의하고 있다.^[7] 자성체에서 자기 모멘트의 원인은 전자의 스핀과 궤도 각운동량 상태이며, 한 영역의 원자가 다른 영역의 원자와 정렬되는지 여부에 따라 달라진다.

=== 자기 극 모델 ===

자기 모멘트는 재료 내에서 정전기학과 유사하게 극으로 표현될 수 있으며, 이를 길버트 모델이라고도 한다.^[8] 이 모델에서 작은 자석은 크기는 같지만 극성이 반대인 한 쌍의 ''가상의'' 자기 단극으로 모델링된다. 각 극은 거리에 따라 약해지는 자기력의 근원이다. 자기 극은 항상 쌍으로 존재하며, 한 극이 끌어당기는 동안 다른 극은 밀어내므로 그 힘은 부분적으로 서로 상쇄된다. 이러한 상쇄는 극이 서로 가까울 때 가장 크다. 막대 자석이 생성하는 자기력은 극의 세기 ''p''(''자기 극 강도'')와 이들을 분리하는 벡터 $\mathbf{\boldsymbol \ell}$ 에 따라 달라진다. 자기 쌍극자 모멘트 '''m'''은 다음과 같이 표현된다.^[7]

$\mathbf{m} = p\,\mathrm{\boldsymbol \ell}\,.$

이는 남극에서 북극 방향으로 향한다. 자기 쌍극자는 각운동량과 관련되어 있기 때문에 전기 쌍극자와의 유추는 주의해야 한다.^[7] 자기 극은 강자성체에 대한 응용 분야에서 정자기 계산에 매우 유용하다. 자기 극 접근 방식을 사용하는 전문가들은 자기장을 회전하지 않는 장 '''H'''로 나타낸다.

=== 앙페르 고리 모델 ===

한스 크리스티안 외르스테드가 전류가 자기장을 생성한다는 것을 발견하고 앙드레 마리 앙페르가 전류가 서로 끌어당기고 밀어낸다는 것을 발견한 후, 모든 자기장이 전류 고리(루프)에 의한 것이라는 가설을 세우는 것은 자연스러운 일이었다. 앙페르가 개발한 이 모형에서 모든 자석을 구성하는 기본적인 자기 쌍극자는 충분히 작은 앙페르 고리 전류 ''I''이다.

앙페르 고리 모형: x에서 페이지 안쪽으로 들어가고 점에서 나오는 전류 고리(루프)는 '''B'''-장(선)을 생성한다. 북극은 오른쪽에 있고 남극은 왼쪽에 있다.

이 고리의 쌍극자 모멘트는 다음과 같다.

:'''m''' = I'''S'''

여기서 '''S'''는 고리(루프)의 면적이다. 자기 모멘트의 방향은 오른손 법칙을 사용하여 전류의 방향과 일치하는 전류로 둘러싸인 면적에 수직인 방향이다.

솔레노이드의 경우 자기 모멘트는 각 회전의 모멘트 벡터 합으로 계산된다. 솔레노이드가 N개의 동일한 회전(단층 권선)과 벡터 면적 '''S'''을 갖는 경우,

:'''m''' = NI'''S'''

=== 양자역학적 모델 ===

물질이나 분자의 자기 모멘트를 미시적 수준에서 계산할 때는, 입자의 각운동량과 자기 모멘트 사이의 선형 관계를 이용한다. 자기 회전비는 자기 모멘트와 각운동량 사이의 관계를 나타낸다.^[25] 앙페르 루프 모델을 사용하여 거시적 전류에 대해서는 간단하게 유도할 수 있지만, 자기 극 모델이나 앙페르 루프 모델 모두 원자 및 분자 수준에서 일어나는 현상을 실제로 나타내는 것은 아니다. 그 수준에서는 양자역학을 사용해야 한다.

모든 물질의 자기 모멘트의 기원은 다음 두 가지이다.

# 물질 내부에서의 전하의 운동(전류)

# 소립자가 고유하게 가지는 자기 모멘트

전자를 기원으로 하는 자기 모멘트는, 계의 내부에 존재하는 모든 전류(혹은 이동하는 전하와 그 속도)의 분포를 조사함으로써 계산할 수 있다. 반면, 후자는 입자가 고유하게 가지는 값이며, 많은 입자에 대해 실험적으로 정밀하게 측정할 수 있다. 예를 들어, 전자의 자기 모멘트는 −9.284764×10⁻²⁴J/T 이다. 자기 모멘트는 벡터량이므로 크기와 방향을 가지지만, 입자의 자기 모멘트의 방향은 입자가 가지는 스핀의 방향에 의해 결정된다.

모든 계의 자기 모멘트는, 계 내에 존재하는 모든 자기 모멘트 벡터의 합으로 표현된다. 예를 들어, 수소 원자(양성자 1개와 전자 1개)의 자기 모멘트는 다음에 열거하는 모든 기여의 벡터의 합이 된다.

전자가 가지는 고유의 자기 모멘트
양성자 주위를 도는 전자의 궤도 운동에 의해 생기는 자기 모멘트
양성자가 가지는 고유의 자기 모멘트

마찬가지로, 자석의 자기 모멘트는 자석 내부의 불쌍전자의 고유의 자기 모멘트와 궤도 자기 모멘트의 합으로 표현할 수 있다.

7. 1. 자기 극 모델

자기 모멘트는 재료 내에서 정전기학과 유사하게 극으로 표현될 수 있으며, 이를 길버트 모델이라고도 한다.^[8] 이 모델에서 작은 자석은 크기는 같지만 극성이 반대인 한 쌍의 ''가상의'' 자기 단극으로 모델링된다. 각 극은 거리에 따라 약해지는 자기력의 근원이다. 자기 극은 항상 쌍으로 존재하며, 한 극이 끌어당기는 동안 다른 극은 밀어내므로 그 힘은 부분적으로 서로 상쇄된다. 이러한 상쇄는 극이 서로 가까울 때 가장 크다. 막대 자석이 생성하는 자기력은 극의 세기 ''p''(''자기 극 강도'')와 이들을 분리하는 벡터

\mathbf{\boldsymbol \ell}

에 따라 달라진다. 자기 쌍극자 모멘트 '''m'''은 다음과 같이 표현된다.^[7]

\mathbf{m} = p\,\mathrm{\boldsymbol \ell}\,.

이는 남극에서 북극 방향으로 향한다. 자기 쌍극자는 각운동량과 관련되어 있기 때문에 전기 쌍극자와의 유추는 주의해야 한다.^[7] 자기 극은 강자성체에 대한 응용 분야에서 정자기 계산에 매우 유용하다. 자기 극 접근 방식을 사용하는 전문가들은 자기장을 회전하지 않는 장 '''H'''로 나타낸다.

7. 2. 앙페르 고리 모델

한스 크리스티안 외르스테드가 전류가 자기장을 생성한다는 것을 발견하고 앙드레 마리 앙페르가 전류가 서로 끌어당기고 밀어낸다는 것을 발견한 후, 모든 자기장이 전류 고리(루프)에 의한 것이라는 가설을 세우는 것은 자연스러운 일이었다. 앙페르가 개발한 이 모형에서 모든 자석을 구성하는 기본적인 자기 쌍극자는 충분히 작은 앙페르 고리 전류 ''I''이다. 이 고리의 쌍극자 모멘트는 다음과 같다.

:'''m''' = I'''S'''

여기서 '''S'''는 고리(루프)의 면적이다. 자기 모멘트의 방향은 오른손 법칙을 사용하여 전류의 방향과 일치하는 전류로 둘러싸인 면적에 수직인 방향이다.

솔레노이드의 경우 자기 모멘트는 각 회전의 모멘트 벡터 합으로 계산된다. 솔레노이드가 N개의 동일한 회전(단층 권선)과 벡터 면적 '''S'''을 갖는 경우,

:'''m''' = NI'''S'''

7. 3. 양자역학적 모델

물질이나 분자의 자기 모멘트를 미시적 수준에서 계산할 때는, 입자의 각운동량과 자기 모멘트 사이의 선형 관계를 이용한다. 자기 회전비는 자기 모멘트와 각운동량 사이의 관계를 나타낸다.^[25] 앙페르 루프 모델을 사용하여 거시적 전류에 대해서는 간단하게 유도할 수 있지만, 자기 극 모델이나 앙페르 루프 모델 모두 원자 및 분자 수준에서 일어나는 현상을 실제로 나타내는 것은 아니다. 그 수준에서는 양자역학을 사용해야 한다.

모든 물질의 자기 모멘트의 기원은 다음 두 가지이다.

# 물질 내부에서의 전하의 운동(전류)

# 소립자가 고유하게 가지는 자기 모멘트

전자를 기원으로 하는 자기 모멘트는, 계의 내부에 존재하는 모든 전류(혹은 이동하는 전하와 그 속도)의 분포를 조사함으로써 계산할 수 있다. 반면, 후자는 입자가 고유하게 가지는 값이며, 많은 입자에 대해 실험적으로 정밀하게 측정할 수 있다. 예를 들어, 전자의 자기 모멘트는 −9.284764×10⁻²⁴J/T 이다. 자기 모멘트는 벡터량이므로 크기와 방향을 가지지만, 입자의 자기 모멘트의 방향은 입자가 가지는 스핀의 방향에 의해 결정된다.

모든 계의 자기 모멘트는, 계 내에 존재하는 모든 자기 모멘트 벡터의 합으로 표현된다. 예를 들어, 수소 원자(양성자 1개와 전자 1개)의 자기 모멘트는 다음에 열거하는 모든 기여의 벡터의 합이 된다.

전자가 가지는 고유의 자기 모멘트
에 의해 생기는 자기 모멘트
양성자가 가지는 고유의 자기 모멘트

마찬가지로, 자석의 자기 모멘트는 자석 내부의 불쌍전자의 고유의 자기 모멘트와 궤도 자기 모멘트의 합으로 표현할 수 있다.

8. 원자, 분자, 소립자의 자기 모멘트

기본적으로 어떤 계의 자기 모멘트에 대한 기여는 두 가지 종류의 원천에서 나올 수 있다. 1) 전류와 같은 전하의 운동; 그리고 2) 전자와 같은 소립자의 스핀으로 인한 고유 자기성.

첫 번째 종류의 원천으로 인한 기여는 계 내부의 모든 전류(또는 모든 전하와 그 속도)의 분포를 알면 계산할 수 있다.

입자 스핀으로 인한 기여는 각 소립자의 고유 자기 모멘트의 크기(종종 실험적으로 매우 정밀하게 측정되는 고정된 수)를 합산한다. 예를 들어, 전자의 자기 모멘트는 −9.284764×10⁻²⁴J/T^[25]로 측정된다. 소립자의 자기 모멘트의 방향은 그 스핀의 방향에 의해 완전히 결정되며, 음의 값은 전자의 자기 모멘트가 스핀과 반평행임을 나타낸다.

어떤 계의 순 자기 모멘트는 하나 또는 두 가지 유형의 원천으로부터의 기여의 벡터 합이다. 예를 들어, 수소-1(양성자와 전자로 구성된 가장 가벼운 수소 동위원소) 원자의 자기 모멘트는 다음 기여의 벡터 합이다.

전자의 고유 모멘트,
양성자 주위의 전자의 궤도 운동,
양성자의 고유 모멘트.

마찬가지로, 막대 자석의 자기 모멘트는 자석 재료의 짝짓지 않은 전자의 고유 및 궤도 자기 모멘트와 핵 자기 모멘트를 포함한 기여하는 자기 모멘트의 합이다.

모든 물질의 자기 모멘트의 기원은 다음 두 가지이다.

# 물질 내부에서의 전하의 운동(전류)

# 소립자가 고유하게 가지는 자기 모멘트

전자를 기원으로 하는 자기 모멘트는, 계의 내부에 존재하는 모든 전류(혹은 이동하는 전하와 그 속도)의 분포를 조사함으로써 계산할 수 있다. 반면, 후자는 입자가 고유하게 가지는 값이며, 많은 입자에 대해 실험적으로 정밀하게 측정할 수 있다. 예를 들어, 전자의 자기 모멘트는 −9.284764×10⁻²⁴J/T^[25]라는 값이 알려져 있다. 자기 모멘트는 벡터량이므로 크기와 방향을 가지지만, 입자의 자기 모멘트의 방향은 입자가 가지는 스핀의 방향에 의해 결정된다. 예를 들어, 전자의 자기 모멘트는 음의 부호를 가지는데, 이것은 전자의 자기 모멘트와 전자의 스핀의 방향이 반평행임을 의미한다.

모든 계의 자기 모멘트는, 계 내에 존재하는 모든 자기 모멘트 벡터의 합으로 표현된다. 예를 들어, 수소 원자(양성자 1개와 전자 1개)의 자기 모멘트는 다음에 열거하는 모든 기여의 벡터의 합이 된다.

전자가 가지는 고유의 자기 모멘트
양성자 주위를 도는 전자의 궤도 운동에 의해 생기는 자기 모멘트
양성자가 가지는 고유의 자기 모멘트

마찬가지로, 자석의 자기 모멘트는 자석 내부의 불쌍전자의 고유의 자기 모멘트와 궤도 자기 모멘트의 합으로 표현할 수 있다.

== 원자의 자기 모멘트 ==

원자의 경우, 개별 전자 스핀을 더하여 총 스핀을 얻고, 개별 궤도 각운동량을 더하여 총 궤도 각운동량을 얻는다. 그런 다음 이 둘을 각운동량 결합을 사용하여 더하여 총 각운동량을 얻는다. 핵 자기 모멘트가 없는 원자의 경우, 원자 쌍극자 모멘트의 크기는 다음과 같다.

:

\mathfrak m_\text{atom} = g_\text{J}\,\mu_\text{B}\,\sqrt{j\,(j+1)\,}

여기서

j

는 총 각운동량 양자수,

g_\text{J}

는 란데 g-인자,

\mu_\text{B}

는 보어 마그네톤이다. 자기장 방향을 따라 이 자기 모멘트의 성분은 다음과 같다.

:

\mathfrak m_{\text{atom},z} = -m\,g_\text{J}\,\mu_\text{B} \, .

음의 부호는 전자가 음전하를 띠기 때문이다.

정수

m

(모멘트

\mathfrak m

와 혼동하지 말 것)는 자기 양자수 또는 '적도' 양자수라고 하며,

2j + 1

개의 값을 가질 수 있다.

:

-j,\ -(j-1),\ \cdots,\ -1,\ 0,\ +1,\ \cdots,\ +(j-1),\ +j~.

각운동량으로 인해 자기장 내 자기 쌍극자의 동역학은 전기장 내 전기 쌍극자의 동역학과 다르다. 자기장은 자기 쌍극자에 토크를 가하여 자기장과 정렬하려고 한다. 그러나 토크는 각운동량 변화율에 비례하므로 세차 운동이 발생한다. 즉, 스핀의 방향이 변한다.

원자 내에 존재하는 모든 전자의 스핀 각운동량과 궤도 각운동량에 대해 각각의 합을 취하고, 각운동량의 합성을 이용하여 총 각운동량을 계산한다. 이때, 원자의 자기 모멘트의 절댓값은

:

m_\text{Atom} = g_J \mu_B \sqrt{J(J+1)}

로 나타낼 수 있다. 여기서, J는 총 각운동량,

g_J

는 란데 g 인자,

\mu_B

는 보어 자기자이다. 이때, 자기장 방향(z축 방향)에 따른 자기 모멘트의 성분은

:

m_\text{Atom}(z) = -m g_J \mu_B

로 나타난다. 이 표기에 나타난 음의 부호는 전자가 음의 전하를 갖는 것에 기인한다. ''m''은 자기 양자수라고 불리며, 아래의

2J + 1

개의 값 중 하나를 취한다.

:

-J, -(J-1), \dots, 0, \dots, +(J-1), +J.

원자의 자기 모멘트는 자기장 속에서 제만 효과를 일으킨다.

== 전자의 자기 모멘트 ==

전자와 많은 기본 입자들은 고유한 자기 모멘트를 가지는데, 이는 양자역학적 처리가 필요하며, 입자의 고유 각운동량과 관련이 있다. 이러한 고유 자기 모멘트는 자기장의 거시적 효과와 전자 상자성 공명과 같은 다른 현상을 일으킨다.

전자의 자기 모멘트는 다음과 같다.

:

'''m'''_S = -g_S * μ_B * '''S''' / ħ

여기서 μ_B은 보어 마그네톤이고, '''S'''는 전자 스핀이며, ħ는 환산 플랑크 상수이다. ''g''_S는 전자 스핀의 g 인자라고 불리며, 디랙 방정식에서 정확히 2라고 예측되지만, 실제로는 양자전기역학에 의한 보정이 더해지기 때문에 약간 어긋난다. 이 어긋남은 이상 자기 모멘트라고 불린다.

위의 등식에 나타나는 음의 부호는 전자의 자기 모멘트와 스핀에 대한 벡터가 반평행임을 의미한다. 만약 스핀 각운동량이 어떤 축 주위를 도는 전자 질량에 의해 발생한다면, 이 회전 운동에 의해 발생하는 고리 모양의 전류는 반대 방향으로 흐른다. 이것은 전자가 음의 전하를 갖기 때문이다. 이러한 고리 모양의 전류는 스핀에 대해 반평행 방향으로 자기 모멘트를 생성한다. 마찬가지로 생각하면, 양전하를 갖는 양전자(전자의 반입자)의 경우에는 자기 모멘트가 스핀과 평행이 된다.

== 핵의 자기 모멘트 ==

핵계는 양성자와 중성자, 즉 핵자로 이루어진 복잡한 물리계이다. 핵자의 양자역학적 성질에는 스핀 등이 포함된다. 핵의 전자기 모멘트는 개별 핵자의 스핀에 의존하기 때문에 핵 모멘트, 보다 구체적으로 핵 자기 쌍극자 모멘트를 측정하여 이러한 성질을 살펴볼 수 있다.

대부분의 일반적인 핵은 바닥 상태에 존재하지만, 일부 동위 원소의 핵은 수명이 긴 여기 상태를 갖는다. 주어진 동위 원소의 핵의 각 에너지 상태는 잘 정의된 자기 쌍극자 모멘트로 특징지어지며, 그 크기는 고정된 숫자이고, 종종 실험적으로 매우 정밀하게 측정된다. 이 값은 핵자의 개별 기여에 매우 민감하며, 그 값의 측정이나 예측은 핵 파동 함수의 내용에 대한 중요한 정보를 드러낼 수 있다. 자기 쌍극자 모멘트의 값을 예측하는 몇 가지 이론적 모델과 핵 차트를 따라 핵에서 측정을 수행하기 위한 여러 가지 실험 기술이 있다.

원자핵은 핵자로 구성되는 복잡한 계이다. 원자핵의 자기 모멘트는 '''핵자기 모멘트'''(nuclear magnetic moment)라고 불리며, 핵자의 운동에 의해 생기는 자기 모멘트와 핵자 자신의 스핀 자기 모멘트에 의해 구성된다.

원자 번호(양성자의 수)가 같은 원자핵이라도, 질량수가 다른 동위원소에서는 다른 자기 모멘트를 보이며, 더 나아가 원자 번호·질량수가 같은 원자핵끼리라도, 그 바닥 상태와 여기 상태에서는 자기 모멘트의 성질에 큰 차이가 생긴다. 알파 입자와 같이 원자 번호와 질량수가 모두 짝수인 원자핵(짝-짝핵)은, 바닥 상태의 스핀이 0이 되기 때문에, 자기 모멘트는 0이다.

원자핵의 자기 모멘트는 핵자기 공명을 일으킨다.

== 분자의 자기 모멘트 ==

분자는 분자의 에너지 준위에 따라 달라질 수 있는, 잘 정의된 자기 모멘트의 크기를 갖는다.^[23] 일반적으로 분자의 전체 자기 모멘트는 다음과 같은 기여의 조합으로 이루어지며, 일반적인 세기 순서대로 나열되어 있다.

짝짓지 않은 전자 스핀(만약 있다면 상자성 기여)으로 인한 자기 모멘트
전자의 궤도 운동. 이는 바닥 상태에서 외부 자기장에 비례하는 경우가 많다(반자성 기여)
핵 스핀의 결합된 자기 모멘트. 이는 핵 스핀 배열에 따라 달라진다.

산소(Oxygen) 분자(O₂)는 가장 바깥쪽 두 전자의 짝짓지 않은 스핀 때문에 강한 상자성(paramagnetism)을 나타낸다. 반면 이산화탄소 분자(CO₂)는 대부분 외부 자기장에 비례하는 전자 분자궤도(Molecular orbital)의 훨씬 약한 자기 모멘트인 반자성(diamagnetism)을 나타낸다. ¹³C 또는 ¹⁷O와 같은 자기 동위원소(isotope)의 핵 자기는 분자의 자기 모멘트에 기여할 것이다. 수소(dihydrogen) 분자(H₂)는 약한(또는 0) 자기장에서 핵 자기(nuclear magnetism)를 나타내며, 파라수소(parahydrogen) 또는 오쏘수소(orthohydrogen) 핵 스핀 배열을 가질 수 있다.

많은 전이 금속 착물(transition metal complexes)이 자성을 띤다. 스핀 전용 공식(spin-only formula)은 첫 번째 열 전이 금속(transition metal)의 고스핀 착물에 대한 좋은 첫 번째 근사치이다.^[23]

짝짓지 않은 전자 수	스핀 전용 모멘트 (μ{{sub)
1	1.73
2	2.83
3	3.87
4	4.90
5	5.92

== 소립자의 자기 모멘트 ==

입자물리학 및 핵물리학 분야에서 소립자나 하드론의 자기 모멘트는 기호 μ로 표시된다.^[24]^[29] 이 경우, 전자의 자기 모멘트의 기본 단위를 보어 마그네톤, 양성자의 자기 모멘트의 기본 단위를 핵 마그네톤이라고 한다.^[24] 입자의 자기 모멘트의 기원은 입자 자체가 갖는 고유의 스핀이나 내부 입자의 궤도 운동으로 해석된다.^[24]^[29]

원자 및 핵물리학에서 그리스 문자 는 입자의 고유 스핀 및/또는 계에서 입자의 궤도 운동과 관련된 자기 모멘트의 크기를 나타내며, 보통 보어 마그네톤 또는 핵 마그네톤으로 측정된다.^[24] 주요 입자가 고유하게 갖는 자기 모멘트의 실험값은 아래 표와 같다.^[29]

일부 기본 입자의 고유 자기 모멘트와 스핀^[24]
입자 이름 (기호)	자기 쌍극자 모멘트 (10 J⋅T)	스핀 양자수 (무차원)
전자 (e⁻)	−9284.764	1/2
양성자 (H⁺)	14.106067	1/2
중성자 (n)	−9.66236	1/2
뮤온 (μ)	−44.904478	1/2
중양성자 (H)	4.3307346	1
트리톤 (H)	15.046094	1/2
헬리온 (He)	−10.746174	1/2
알파 입자 (He)	0	0

주요 입자의 자기 모멘트와 스핀^[29]
입자명	자기 모멘트(10 J⋅T)	스핀
전자	−928.476 4620(57)	1/2
양성자	1.410 606 7873(97)	1/2
중성자	−0.966 236 50(23)	1/2
뮤온	−4.490 448 26(10)	1/2
중수소 원자핵	0.433 073 5040(36)	1
삼중수소 원자핵	1.504 609 503(12)	1/2
헬륨-3 원자핵	−1.074 617 522(14)	1/2
알파 입자	0	0

8. 1. 원자의 자기 모멘트

원자의 경우, 개별 전자 스핀을 더하여 총 스핀을 얻고, 개별 궤도 각운동량을 더하여 총 궤도 각운동량을 얻는다. 그런 다음 이 둘을 각운동량 결합을 사용하여 더하여 총 각운동량을 얻는다. 핵 자기 모멘트가 없는 원자의 경우, 원자 쌍극자 모멘트의 크기

\mathfrak m_\text{atom}

는 다음과 같다.

:

\mathfrak m_\text{atom} = g_\text{J}\,\mu_\text{B}\,\sqrt{j\,(j+1)\,}

여기서

j

는 총 각운동량 양자수,

g_\text{J}

는 란데 g-인자,

\mu_\text{B}

는 보어 마그네톤이다. 자기장 방향을 따라 이 자기 모멘트의 성분은 다음과 같다.

:

\mathfrak m_{\text{atom},z} = -m\,g_\text{J}\,\mu_\text{B} \, .

음의 부호는 전자가 음전하를 띠기 때문이다.

정수

m

(모멘트

\mathfrak m

와 혼동하지 말 것)는 자기 양자수 또는 '적도' 양자수라고 하며,

2j + 1

개의 값을 가질 수 있다.

:

-j,\ -(j-1),\ \cdots,\ -1,\ 0,\ +1,\ \cdots,\ +(j-1),\ +j~.

각운동량으로 인해 자기장 내 자기 쌍극자의 동역학은 전기장 내 전기 쌍극자의 동역학과 다르다. 자기장은 자기 쌍극자에 토크를 가하여 자기장과 정렬하려고 한다. 그러나 토크는 각운동량 변화율에 비례하므로 세차 운동이 발생한다. 즉, 스핀의 방향이 변한다. 이러한 거동은 란다우-리프시츠-길버트 방정식으로 설명된다.

:

\frac{1}{\gamma} \frac{\mathrm d\mathbf{m}}{\mathrm dt} = \mathbf{m} \times \mathbf{H}_\text{eff} - \frac{\lambda}{\gamma m} \mathbf{m} \times \frac{\mathrm d\mathbf{m}}{\mathrm dt}

여기서

\gamma

는 자기 회전 비,

\mathbf{m}

는 자기 모멘트,

\lambda

는 감쇠 계수,

\mathbf{H}_\text{eff}

는 유효 자기장(외부 자기장과 자체 유도 자기장의 합)이다. 첫 번째 항은 유효 자기장에 대한 모멘트의 세차 운동을 설명하고, 두 번째 항은 주변과의 상호 작용으로 인한 에너지 소산과 관련된 감쇠 항이다.

원자 내에 존재하는 모든 전자의 스핀 각운동량과 궤도 각운동량에 대해 각각의 합을 취하고, 각운동량의 합성을 이용하여 총 각운동량을 계산한다. 이때, 원자의 자기 모멘트의 절댓값은

:

m_\text{Atom} = g_J \mu_B \sqrt{J(J+1)}

로 나타낼 수 있다. 여기서, J는 총 각운동량,

g_J

는 란데 g 인자,

\mu_B

는 보어 자기자이다. 이때, 자기장 방향(z축 방향)에 따른 자기 모멘트의 성분은

:

m_\text{Atom}(z) = -m g_J \mu_B

로 나타난다. 이 표기에 나타난 음의 부호는 전자가 음의 전하를 갖는 것에 기인한다. ''m''은 자기 양자수라고 불리며, 아래의

2J + 1

개의 값 중 하나를 취한다.

:

-J, -(J-1), \dots, 0, \dots, +(J-1), +J.

원자의 자기 모멘트는 자기장 속에서 제만 효과를 일으킨다.

8. 2. 전자의 자기 모멘트

전자와 많은 기본 입자들은 고유한 자기 모멘트를 가지는데, 이는 양자역학적 처리가 필요하며, 입자의 고유 각운동량과 관련이 있다. 이러한 고유 자기 모멘트는 자기장의 거시적 효과와 전자 상자성 공명과 같은 다른 현상을 일으킨다.

전자의 자기 모멘트는 다음과 같다.

:

'''m'''_S = -g_S * μ_B * '''S''' / ħ

여기서 μ_B은 보어 마그네톤이고, '''S'''는 전자 스핀이며, ħ는 환산 플랑크 상수이다. ''g''_S는 전자 스핀의 g 인자라고 불리며, 디랙 방정식에서 정확히 2라고 예측되지만, 실제로는 양자전기역학에 의한 보정이 더해지기 때문에 약간 어긋난다. 이 어긋남은 이상 자기 모멘트라고 불린다.

위의 등식에 나타나는 음의 부호는 전자의 자기 모멘트와 스핀에 대한 벡터가 반평행임을 의미한다. 만약 스핀 각운동량이 어떤 축 주위를 도는 전자 질량에 의해 발생한다면, 이 회전 운동에 의해 발생하는 고리 모양의 전류는 반대 방향으로 흐른다. 이것은 전자가 음의 전하를 갖기 때문이다. 이러한 고리 모양의 전류는 스핀에 대해 반평행 방향으로 자기 모멘트를 생성한다. 마찬가지로 생각하면, 양전하를 갖는 양전자(전자의 반입자)의 경우에는 자기 모멘트가 스핀과 평행이 된다.

8. 3. 핵의 자기 모멘트

핵계는 양성자와 중성자, 즉 핵자로 이루어진 복잡한 물리계이다. 핵자의 양자역학적 성질에는 스핀 등이 포함된다. 핵의 전자기 모멘트는 개별 핵자의 스핀에 의존하기 때문에 핵 모멘트, 보다 구체적으로 핵 자기 쌍극자 모멘트를 측정하여 이러한 성질을 살펴볼 수 있다.

대부분의 일반적인 핵은 바닥 상태에 존재하지만, 일부 동위 원소의 핵은 수명이 긴 여기 상태를 갖는다. 주어진 동위 원소의 핵의 각 에너지 상태는 잘 정의된 자기 쌍극자 모멘트로 특징지어지며, 그 크기는 고정된 숫자이고, 종종 실험적으로 매우 정밀하게 측정된다. 이 값은 핵자의 개별 기여에 매우 민감하며, 그 값의 측정이나 예측은 핵 파동 함수의 내용에 대한 중요한 정보를 드러낼 수 있다. 자기 쌍극자 모멘트의 값을 예측하는 몇 가지 이론적 모델과 핵 차트를 따라 핵에서 측정을 수행하기 위한 여러 가지 실험 기술이 있다.

원자핵은 핵자로 구성되는 복잡한 계이다. 원자핵의 자기 모멘트는 '''핵자기 모멘트'''(nuclear magnetic moment)라고 불리며, 핵자의 운동에 의해 생기는 자기 모멘트와 핵자 자신의 스핀 자기 모멘트에 의해 구성된다.

원자 번호(양성자의 수)가 같은 원자핵이라도, 질량수가 다른 동위원소에서는 다른 자기 모멘트를 보이며, 더 나아가 원자 번호·질량수가 같은 원자핵끼리라도, 그 바닥 상태와 여기 상태에서는 자기 모멘트의 성질에 큰 차이가 생긴다. 알파 입자와 같이 원자 번호와 질량수가 모두 짝수인 원자핵(짝-짝핵)은, 바닥 상태의 스핀이 0이 되기 때문에, 자기 모멘트는 0이다.

원자핵의 자기 모멘트는 핵자기 공명을 일으킨다.

8. 4. 분자의 자기 모멘트

분자는 분자의 에너지 준위에 따라 달라질 수 있는, 잘 정의된 자기 모멘트의 크기를 갖는다.^[23] 일반적으로 분자의 전체 자기 모멘트는 다음과 같은 기여의 조합으로 이루어지며, 일반적인 세기 순서대로 나열되어 있다.

짝짓지 않은 전자 스핀(만약 있다면 상자성 기여)으로 인한 자기 모멘트
전자의 궤도 운동. 이는 바닥 상태에서 외부 자기장에 비례하는 경우가 많다(반자성 기여)
핵 스핀의 결합된 자기 모멘트. 이는 핵 스핀 배열에 따라 달라진다.

산소(Oxygen) 분자(O₂)는 가장 바깥쪽 두 전자의 짝짓지 않은 스핀 때문에 강한 상자성(paramagnetism)을 나타낸다. 반면 이산화탄소 분자(CO₂)는 대부분 외부 자기장에 비례하는 전자 분자궤도(Molecular orbital)의 훨씬 약한 자기 모멘트인 반자성(diamagnetism)을 나타낸다. ¹³C 또는 ¹⁷O와 같은 자기 동위원소(isotope)의 핵 자기는 분자의 자기 모멘트에 기여할 것이다. 수소(dihydrogen) 분자(H₂)는 약한(또는 0) 자기장에서 핵 자기(nuclear magnetism)를 나타내며, 파라수소(parahydrogen) 또는 오쏘수소(orthohydrogen) 핵 스핀 배열을 가질 수 있다.

많은 전이 금속 착물(transition metal complexes)이 자성을 띤다. 스핀 전용 공식(spin-only formula)은 첫 번째 열 전이 금속(transition metal)의 고스핀 착물에 대한 좋은 첫 번째 근사치이다.^[23]

짝짓지 않은 전자 수	스핀 전용 모멘트 (μ{{sub)
1	1.73
2	2.83
3	3.87
4	4.90
5	5.92

8. 5. 소립자의 자기 모멘트

입자물리학 및 핵물리학 분야에서 소립자나 하드론의 자기 모멘트는 기호 μ로 표시된다.^[24]^[29] 이 경우, 전자의 자기 모멘트의 기본 단위를 보어 마그네톤, 양성자의 자기 모멘트의 기본 단위를 핵 마그네톤이라고 한다.^[24] 입자의 자기 모멘트의 기원은 입자 자체가 갖는 고유의 스핀이나 내부 입자의 궤도 운동으로 해석된다.^[24]^[29]

원자 및 핵물리학에서 그리스 문자 는 입자의 고유 스핀 및/또는 계에서 입자의 궤도 운동과 관련된 자기 모멘트의 크기를 나타내며, 보통 보어 마그네톤 또는 핵 마그네톤으로 측정된다.^[24] 주요 입자가 고유하게 갖는 자기 모멘트의 실험값은 아래 표와 같다.^[29]

일부 기본 입자의 고유 자기 모멘트와 스핀^[24]
입자 이름 (기호)	자기 쌍극자 모멘트 (10 J⋅T)	스핀 양자수 (무차원)
전자 (e⁻)		1/2
양성자 (H⁺)		1/2
중성자 (n)		1/2
뮤온 (μ)		1/2
중양성자 (H)		1
트리톤 (H)		1/2
헬리온 (He)		1/2
알파 입자 (He)	0	0

주요 입자의 자기 모멘트와 스핀^[29]
입자명	자기 모멘트(10 J⋅T)	스핀
전자	−928.476 4620(57)	1/2
양성자	1.410 606 7873(97)	1/2
중성자	−0.966 236 50(23)	1/2
뮤온	−4.490 448 26(10)	1/2
중수소 원자핵	0.433 073 5040(36)	1
삼중수소 원자핵	1.504 609 503(12)	1/2
헬륨-3 원자핵	−1.074 617 522(14)	1/2
알파 입자	0	0

9. 외부 자기장 효과

외부 자기장이 존재할 때, 자기 모멘트는 자기장으로부터 토크를 받는다. 이 토크에 의해 발생하는 세차운동은 라모어 세차라 불리며, 그 운동 방정식은

: $\frac{1}{\gamma} \frac{\mathrm{d}\boldsymbol{m}}{\mathrm{d}t} = \boldsymbol{m} \times \boldsymbol{H}$

로 나타낼 수 있다. 여기서, '''m'''은 자기 모멘트, '''H'''는 자기장, γ는 자기 회전 비율이다.

이에 더하여, 실제 물질 내의 세차운동은 시간이 지남에 따라 감쇠한다. 이러한 거동은 란다우-리프시츠-길버트 방정식에 의해 기술된다.^[30]^[31]

: $\frac{1}{\gamma} \frac{\mathrm{d}\boldsymbol{m}}{\mathrm{d}t} = \boldsymbol{m} \times \boldsymbol{H}_{\text{eff}} - \frac{\lambda}{\gamma m}\boldsymbol{m} \times \frac{\mathrm{d}\boldsymbol{m}}{\mathrm{d}t}.$

여기서, '''H'''_eff는 유효 자기장(외부 자기장 + 자체 자기장 + 양자역학적 보정), λ는 감쇠 운동의 크기를 결정하는 계수이다. 우변 제1항은 유효 자기장에 의한 자기 모멘트의 세차 운동을 나타내고, 제2항은 주위와의 상호작용에 의한 에너지 손실을 나타내는 감쇠항이다.

9. 1. 자기 모멘트에 작용하는 힘

외부에서 생성된 자기장 내의 자기 모멘트는 다음과 같은 퍼텐셜 에너지 를 갖는다.

:

U = -\mathbf{m}\cdot\mathbf{B}

외부 자기장이 균일하지 않은 경우, 자기 모멘트 자체에 작용하는 힘이 자기장 기울기에 비례하여 발생한다. 자기 쌍극자에 작용하는 힘에 대한 두 가지 표현이 있는데, 쌍극자에 사용된 모델이 전류 고리인지 또는 두 개의 단극(전기 쌍극자와 유사)인지에 따라 다르다.^[10] 전류 고리 모델의 경우 힘은 다음과 같다.

:

\mathbf{F}_\text{loop}=\nabla \left(\mathbf{m}\cdot\mathbf{B}\right) .

자기 단극의 존재를 가정하면 힘은 다음과 같이 수정된다.

:

\begin{align}\mathbf{F}_\text{loop} &= \left(\mathbf{m}\times\nabla\right) \times \mathbf{B} \\[1ex]&= \nabla \left(\mathbf{m}\cdot\mathbf{B}\right) - \left(\nabla\cdot\mathbf{B}\right) \mathbf{m}\end{align}

단극 쌍을 사용하는 경우(즉, 전기 쌍극자 모델), 힘은 다음과 같다.

:

\mathbf{F}_\text{dipole} = \left(\mathbf{m} \cdot \nabla \right) \mathbf{B}.

그리고 다음 관계를 통해 서로 표현할 수 있다.

:

\mathbf{F}_\text{loop}=\mathbf{F}_\text{dipole} + \mathbf{m}\times \left(\nabla \times \mathbf{B} \right) - \left(\nabla\cdot\mathbf{B}\right) \mathbf{m}.

이러한 모든 식에서 은 쌍극자이고 는 해당 위치의 자기장이다. 전류나 시간에 따라 변하는 전기장 또는 자기 전하가 없는 경우, , 이고 두 표현이 일치한다.

외부 자기장이 존재할 때, 자기 모멘트는 자기장으로부터 토크를 받는다. 이 토크에 의해 발생하는 세차운동은 라모어 세차라 불리며, 그 운동 방정식은

:

\frac{1}{\gamma} \frac{\mathrm{d}\boldsymbol{m}}{\mathrm{d}t} = \boldsymbol{m} \times \boldsymbol{H}

로 나타낼 수 있다. 여기서, '''m'''은 자기 모멘트, '''H'''는 자기장, γ는 자기 회전 비율이다.

이에 더하여, 실제 물질 내의 세차운동은 시간이 지남에 따라 감쇠한다. 이러한 거동은 란다우-리프시츠-길버트 방정식에 의해 기술된다.^[30]^[31]

:

\frac{1}{\gamma} \frac{\mathrm{d}\boldsymbol{m}}{\mathrm{d}t} = \boldsymbol{m} \times \boldsymbol{H}_{\text{eff}} - \frac{\lambda}{\gamma m}\boldsymbol{m} \times \frac{\mathrm{d}\boldsymbol{m}}{\mathrm{d}t}.

여기서, '''H'''_eff는 유효 자기장(외부 자기장 + 자체 자기장 + 양자역학적 보정), λ는 감쇠 운동의 크기를 결정하는 계수이다. 우변 제1항은 유효 자기장에 의한 자기 모멘트의 세차 운동을 나타내고, 제2항은 주위와의 상호작용에 의한 에너지 손실을 나타내는 감쇠항이다.

9. 2. 자유 에너지와의 관계

균일한 자기장 '''B'''에서, 자유 에너지 ''F''는 계의 자기 모멘트 '''M'''과 다음과 같이 관련될 수 있다.^[11]

:

\mathrm dF = -S\,\mathrm dT - \mathbf{M}\,\cdot \mathrm d\mathbf{B}

여기서 ''S''는 계의 엔트로피이고 ''T''는 온도이다. 따라서, 자기 모멘트는 계의 자유 에너지 측면에서 다음과 같이 정의될 수도 있다.

:

m = \left. - \frac{\partial F}{\partial B}  \right|_{T}.

9. 3. 자성

가해진 자기장은 물체 자체의 자기 모멘트를 변화시킬 수 있는데, 예를 들어 물체를 자화시키는 경우가 해당된다. 이 현상은 자기로 알려져 있다. 가해진 자기장은 물질을 구성하는 자기 쌍극자를 뒤집을 수 있으며, 이는 상자성과 강자성을 모두 유발한다. 게다가, 자기장은 자기장을 생성하는 전류(원자 궤도와 같은)에 영향을 미칠 수 있으며, 이는 반자성을 유발한다.

10. 자기 쌍극자 간의 상호작용

10. 1. 두 자기 쌍극자 사이의 힘

앞서 논의했듯이, 자기 모멘트 '''m'''₁을 가진 쌍극자 루프가 자기 모멘트 '''m'''₂을 가진 다른 쌍극자 루프에 작용하는 힘은 다음과 같다.^[12]^[13]

\mathbf F = \nabla \left(\mathbf m_2 \cdot \mathbf B_1\right),

여기서 '''B'''₁은 자기 모멘트 '''m'''₁에 의한 자기장이다. 기울기 계산 결과는 다음과 같다.

\mathbf F(\mathbf r,\mathbf m_1,\mathbf m_2) = \frac{3\mu_0}{4\pi|\mathbf r|^4} \left[\mathbf m_2 (\mathbf m_1\cdot\hat\mathbf r) + \mathbf m_1(\mathbf m_2\cdot\hat\mathbf r) + \hat\mathbf r(\mathbf m_1\cdot\mathbf m_2) - 5\hat\mathbf r(\mathbf m_1\cdot\hat\mathbf r)(\mathbf m_2\cdot\hat\mathbf r)\right],

여기서 '''r̂'''은 자석 1에서 자석 2로 향하는 단위 벡터이고 ''r''은 거리이다. 동등한 표현은 다음과 같다.

\mathbf F = \frac{3\mu_0}{4\pi|\mathbf r|^4} \left[(\hat\mathbf r\times\mathbf m_1)\times\mathbf m _2 + (\hat\mathbf r\times\mathbf m_2)\times\mathbf m_1 - 2 \hat\mathbf r(\mathbf m_1 \cdot \mathbf m_2 ) + 5\hat\mathbf r(\hat\mathbf r\times\mathbf m_1)\cdot(\hat\mathbf r\times\mathbf m_2)\right].

'''m'''₁에 작용하는 힘은 반대 방향이다.

10. 2. 토크

자석 1이 자석 2에 작용하는 토크는 다음과 같다.

:

\boldsymbol\tau = \mathbf m_2 \times \mathbf B_1.

11. 자기 쌍극자의 이론적 배경

자기 쌍극자 모멘트는 다극 전개의 한 항으로, 자기 단극, 자기 쌍극자, 사중극자 등과 함께 자기장을 모델링하는 데 사용된다. 각 항의 자기장 크기는 거리에 따라 감소하며, 충분히 먼 거리에서는 첫 번째 영이 아닌 항이 지배적이다. 많은 자석의 경우 첫 번째 영이 아닌 항은 자기 쌍극자 모멘트이다.

자기 쌍극자 모멘트는 자기 퍼텐셜^[9]을 이용하여 수학적으로 기술할 수 있다. 자기 극 모델에서는 탈자장 $\mathbf{H}$ 와 자기 스칼라 퍼텐셜을, 앙페르 루프 모델에서는 자기 유도 $\mathbf{B}$ 와 자기 벡터 퍼텐셜을 사용한다.

전류 분포가 충분히 작은 영역에 한정된다는 조건 하에, 벡터 퍼텐셜의 첫 번째 영이 아닌 항은 다음과 같다.

: $\mathbf{A}(\mathbf r) = \frac{\mu_0}{4\pi} \frac{\mathbf m\times\mathbf r}$

12. 각운동량과의 관계

자기 모멘트는 각운동량과 밀접한 관련이 있으며, 이를 자기 회전 효과라고 한다. 이 효과는 거시적 규모에서 아인슈타인-더하스 효과(자화에 의한 회전)와 그 역효과인 바네트 효과(회전에 의한 자화)로 나타난다.^[1] 원자핵과 같이 상대적으로 고립된 자기 쌍극자에 토크를 가하면 세차 운동(가해진 자기장 축을 중심으로 회전)을 일으킬 수 있다.자기 쌍극자를 전류 고리로 보면 자기 모멘트와 각운동량 사이의 관계를 알 수 있다. 자기 회전비(

\gamma

)는 자기 모멘트와 각운동량의 비율이며,^[14]^[15] 앙페르 고리 모델에서 자기 회전비는 전하-질량 비의 절반이다. 움직이는 대전 입자의 각운동량은

\mathbf{L} = \mathbf{r}\times\mathbf{p} = \mu \, \mathbf{r}\times\mathbf{v}

로 정의되며, 여기서 는 입자의 질량, 는 입자의 속도이다. 전류를 구성하는 매우 많은 수의 대전 입자의 각운동량은

\mathbf{L} = \iiint_V \, \mathbf{r} \times (\rho \mathbf{v})\, \mathrm dV\,

이며, 여기서 는 움직이는 입자의 질량 밀도이다.^[16]

이에 대응하는 자기 모멘트는

\mathbf{m} = \tfrac{1}{2}\iiint_V \mathbf{r} \times (\rho_{Q} \mathbf{v})\, \mathrm dV\,

이며, 여기서

\mathbf{j} = \rho_Q \mathbf{v}

이고

\rho_Q

는 움직이는 대전 입자의 전하 밀도이다. 두 방정식을 비교하면

\mathbf{m} = \frac{e}{2\mu}\,\mathbf{L}\,

을 얻으며, 여기서

e

는 입자의 전하,

\mu

는 입자의 질량이다.

원자 입자는 균일한 전하-질량 비의 궤도 및 스핀 전하 분포로 정확하게 설명할 수 없지만, 원자 세계에서

\mathbf{m} = g \, \frac{e}{2\mu} \, \mathbf{L}

경향이 관찰되며, 여기서 -인자는 입자와 구성에 따라 달라진다. 원자 세계에서 입자의 각운동량(스핀)은 환산 플랑크 상수 의 정수(혹은 페르미온의 경우 반정수) 배수이며, 보어 마그네톤 및 핵 마그네톤의 자기 모멘트 단위를 정의하는 기준이 된다.

외부 자기장이 존재할 때, 자기 모멘트는 자기장으로부터 토크를 받는다. 이 토크에 의해 발생하는 세차운동은 라모어 세차라 불리며, 그 운동 방정식은

\frac{1}{\gamma} \frac{\mathrm{d}\boldsymbol{m}}{\mathrm{d}t} = \boldsymbol{m} \times \boldsymbol{H}

로 나타낼 수 있다. 여기서, '''m'''은 자기 모멘트, '''H'''는 자기장, γ는 자기 회전 비율이다. 실제 물질 내의 세차운동은 시간이 지남에 따라 감쇠하며, 이는 란다우-리프시츠-길버트 방정식에 의해 기술된다.^[30]^[31]

13. 같이 보기

14. 외부 링크

15. 참고 문헌

16. 각주

참조

_[1] 서적 Introduction to Magnetic Materials https://books.google[...] Wiley-IEEE Press
_[2] 서적 Thermodynamics and an Introduction to Thermostatistics https://archive.org/[...] John Wiley & Sons
_[3] 웹사이트 Magnetic units http://www.ieeemagne[...] IEEE Magnetics 2016-02-19
_[4] 논문 CODATA Recommended Values of the Fundamental Physical Constants: 2014 2015-07-21
_[5] 간행물 SIbrochure9th
_[6] 웹사이트 K&J Magnetics – Glossary https://www.kjmagnet[...]
_[7] 서적 Magnetostatic Principles in Ferromagnetism North-Holland
_[8] 서적 Introduction to Electrodynamics Prentice Hall
_[9] 서적 Classical Electrodynamics https://archive.org/[...] Wiley
_[10] 논문 The Force on a Magnetic Dipole
_[11] 서적 Electrodynamics of Continuous Media: Volume 8 (Course of Theoretical Physics) Butterworth-Heinemann 1984-01-15
_[12] 서적 Permanent Magnet and Electromechanical Devices: Materials, Analysis, and Applications https://books.google[...] Academic Press
_[13] 논문 An Analytic Solution for the Force between Two Magnetic Dipoles http://downloads.hin[...] 2012-11-24
_[14] 서적 Basic Theoretical Physics https://books.google[...] Springer
_[15] 서적 Introduction to functional magnetic resonance imaging https://books.google[...] Cambridge University Press
_[16] 서적 The Feynman Lectures on Physics Pearson/Addison-Wesley
_[17] 웹사이트 CODATA Value: electron magnetic moment https://physics.nist[...]
_[18] 서적 Understanding Solids https://books.google[...] John Wiley and Sons
_[19] 서적 Modern Physics https://books.google[...] Macmillan
_[20] 서적 Ions, Electrons, and Ionizing Radiations https://archive.org/[...] Edward Arnold
_[21] 서적 Advances in chemical physics https://books.google[...] Wiley
_[22] 서적 Micromagnetism and Electrical Resistance of Ferromagnetic Electrodes for Spin Injection Devices https://books.google[...] Cuvillier Verlag
_[23] 백과사전 The magnetochemistry of complex compounds https://archive.org/[...] Interscience 1960
_[24] 웹사이트 Search results matching 'magnetic moment' http://physics.nist.[...] National Institute of Standards and Technology 2012-05-11
_[25] 웹사이트 CODATA Value: electron magnetic moment http://physics.nist.[...] 2012-06-16
_[26] 서적 Understanding Solids https://books.google[...] John Wiley and Sons 2012-06-16
_[27] 서적 Modern Physics https://books.google[...] Macmillan Publishers (United States) 2012-06-16
_[28] 서적 Ions, Electrons and Ionizing Radiations https://books.google[...] Rene Press 2012-06-16
_[29] 웹사이트 CODATA Values of the Fundamental Constants http://physics.nist.[...] NIST 2015-07-03
_[30] 서적 Advances in chemical physics https://books.google[...] John Wiley & Sons 2012-06-16
_[31] 서적 Micromagnetism and Electrical Resistance of Ferromagnetic Electrodes for Spin Injection Devices https://books.google[...] Cuvillier Verlag 2012-06-16

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com